前面我发过一篇文章，探讨的是带宽和上升时间的系数0.35是怎么来的？

Part1

$$ \displaystyle BW = \frac{0.35}{Tr} $$

虽然我们找到了这个系数关系，确实是在0.35~0.4之间。其实当时我留有疑问，我发现随着方波分解的次数变多（几万次），最高频率fmax也在增加，上升时间Tr也在加快，但是“0.35”这个系数不稳了。

Part 02

我们复盘一下当时的做法：

首先，用傅里叶级数（FS）分解方波，

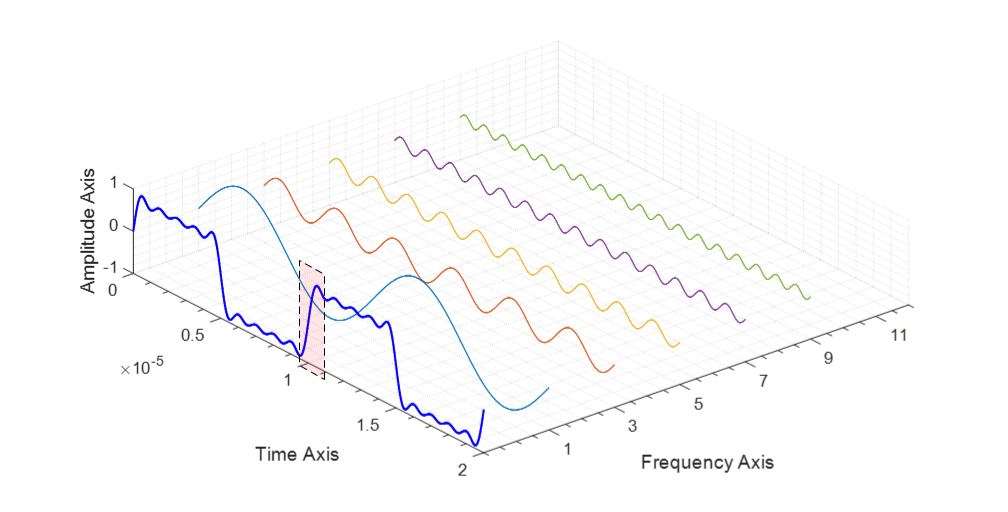
然后，逐渐增大谐波次数，获得最高次谐波的频率fmax，找出此时合成方波边沿10-90%的上升时间Tr，

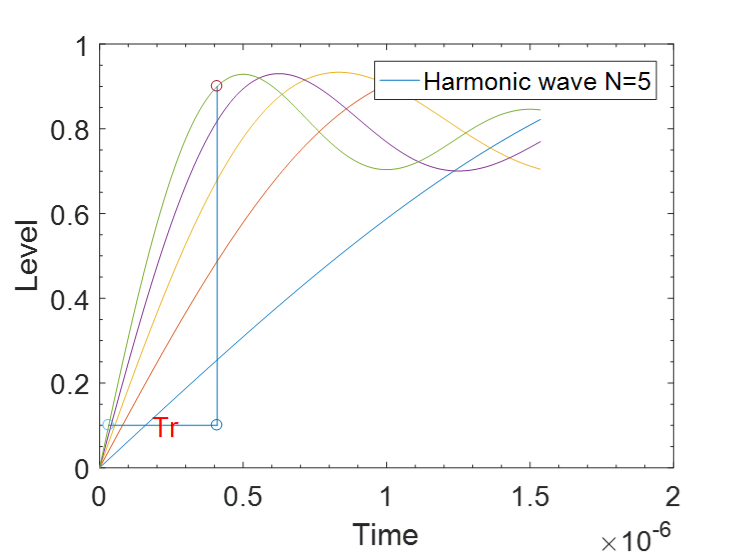
最后，对这些谐波fmax和对应合成波的Tr做乘积，找出他们的系数关系。

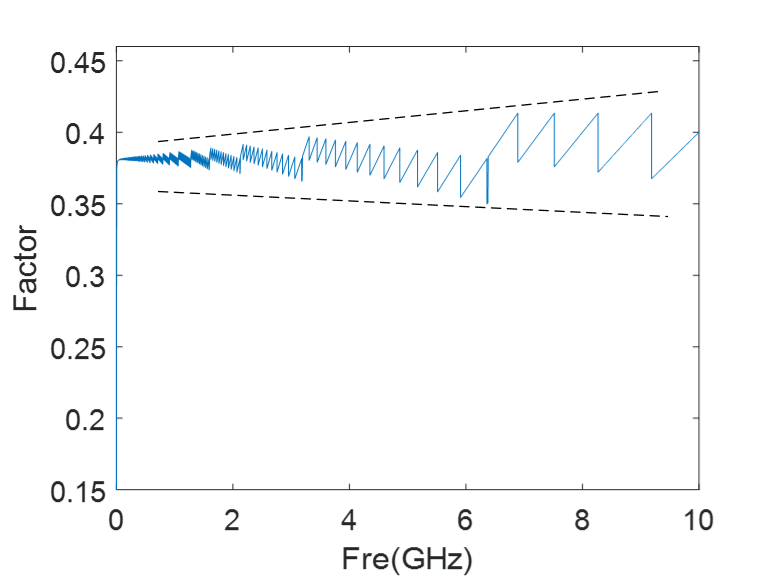
很漂亮的值！趋于0.35。但是当我逐渐继续提高分解的次数，fmax变大，Tr变小，它们的乘积，不再是“0.35”。

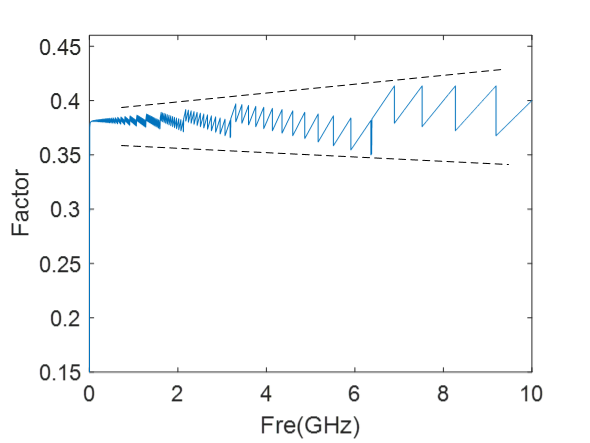
感觉它在发散，而且那个“锯齿波”，像极了S参数里的相位逐渐递增，强迫纠正到主值区间的图。

所以那篇文章我用委婉的语气用了一个“大概”，

所以这个0.35大概就是通过分解方波信号，通过FS求得子信号的最高频率和此时信号的上升沿，去拟合出来的一个值。

Part 03

本来这个问题当时就不打算研究了，我甚至一度怀疑自己的做法错了，伯格丁的书，也只是用语言描述了这种经验公式的由来。

直到昨天后台有个同学问我要了下源码，我重新review了下流程，观察数据后，找到了问题，matlab代码上设置的采样率不够，随着分解次数，信号频率fmax增大，边沿Tr加快后，matlab判断的时候稳态值>0.1和>0.9，两个t重合，获取不到Tr。

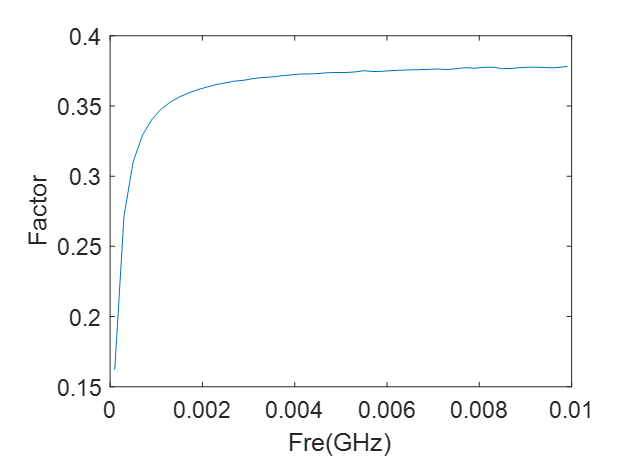
提高Fs采样率后，问题得以解释清楚，虽然还有一点发散，但是不影响，10G以内，公式正确！

我们最后看一下波图，

采样率低：

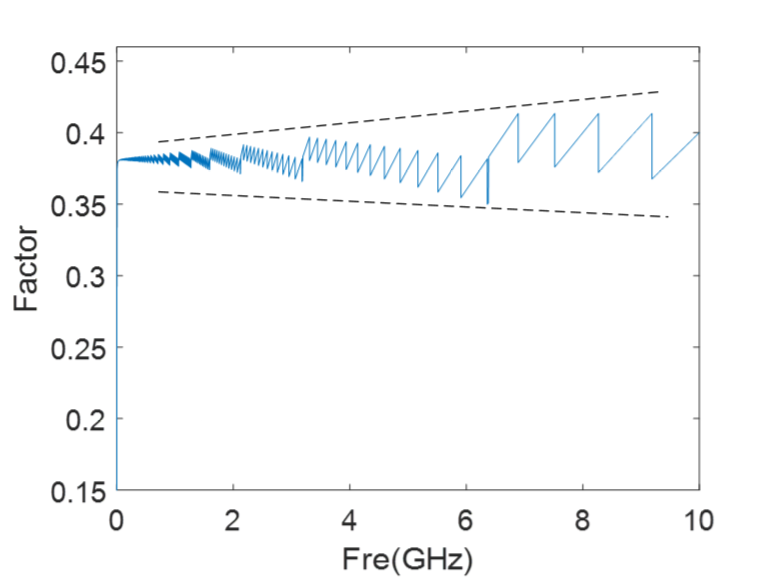
提高采样率：

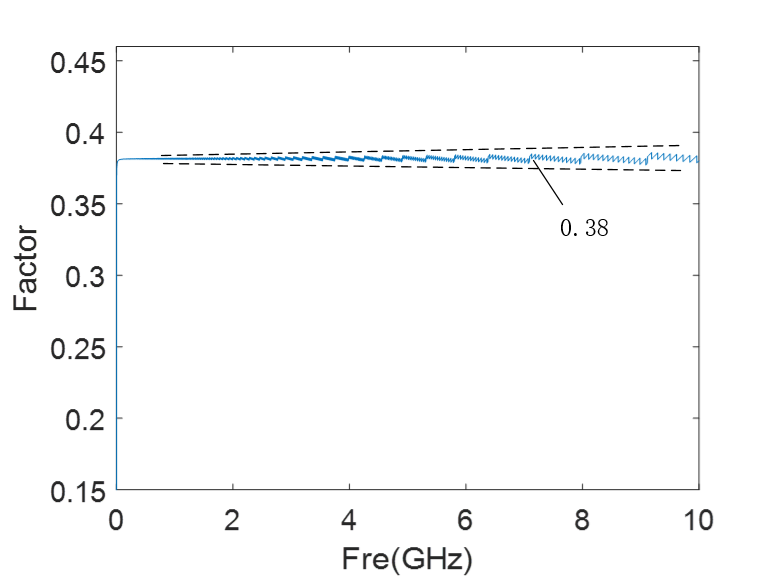
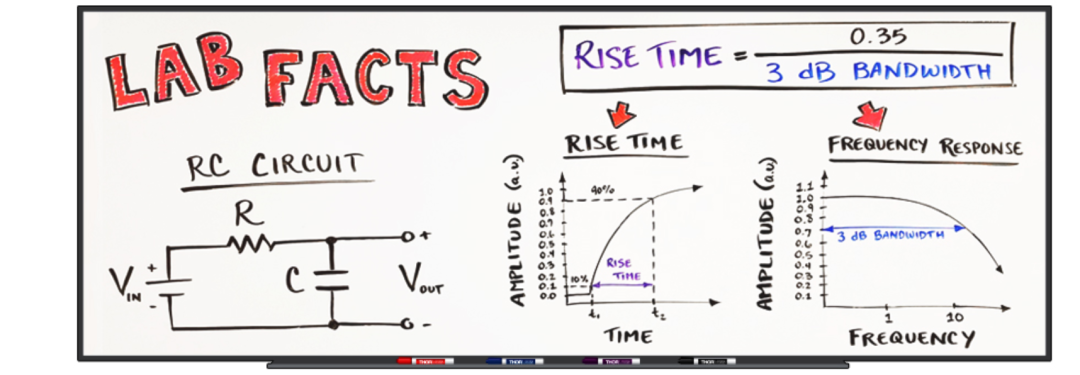
这个0.38很漂亮，用一张索雷博的公式漫画：

Part 04

随着方波分解次数提高，信号边沿几乎垂直，如果还是想要观察边沿的细节，这时对采样率提出了极高的要求，code里面观察10G的信号，我的采样率已经设置到了2000G。